3.5 Limits at Infinity

• Determine finite limits at infinity.

• Determine horizontal asymptotes of the graph of  a function. ( if any)

• Determine infinite limits at infinity.

HOMEWORK

Page 205 3-8, 10, 13, 15-33 odd

http://www.larsoncalculus.com/etf6/content/calculus-videos/chapter-4/section-5/limitsatinfinity/#content-top

3.6 Finish graphs of rational functions

Oblique or Slant Asymptote If the degree of the numerator is one more than the degree of the denominator, then the graph of the rational function will have a slant asymptote.

http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut40_ratgraph.htm

Some things to note: The slant asymptote is the quotient part of the answer you get when you divide the numerator by the denominator.If you need a review of long division, feel free to go to Tutorial 36: Long Division. You may have 0 or 1 slant asymptote,  but no more than that. A graph can have both a vertical and a slant asymptote, but it CANNOT have both a horizontal and slant asymptote. You draw a slant asymptote on the graph by putting a dashed horizontal (left and right) line going through y = mx + b. Below is an example of a slant asymptote of y = x + 1:

Example 6: Find the oblique asymptote of the function .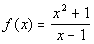

Note that this rational function is already reduced down. Applying long division to this problem we get:

. The equation for the slant asymptote is the quotient part of the answer which would be  .

Graphing Rational Functions

Step 1: Reduce the rational function to lowest terms and check for any open holes in the graph.

If any factors are TOTALLY removed from the denominator, then there will not be a vertical asymptote through that value, but an open hole at that point. If this is the case, plug in the x value that causes that removed factor to be zero into the reduced rational function.  Plot this point as an open hole.

Step 2: Find all of the asymptotes and draw them as dashed lines.

Let   be a rational function reduced to lowest terms and Q(x) has a degree of at least 1: There is a vertical asymptote for every root of   . There is a horizontal asymptote of y = 0 (x-axis) if the degree of P(x) < the degree of Q(x). There is a horizontal asymptote of   if the degree of P(x) = the degree of Q(x). There is an oblique or slant asymptote if the degree of P(x) is one degree higher than Q(x).  If this is the case the oblique asymptote is the quotient part of the division. Note that a graph can have both a vertical and a slant asymptote, or both a vertical and horizontal asymptote, but it CANNOT have both a horizontal and slant asymptote.

Step 3: Determine the symmetry.

The graph is symmetric about the y-axis if the function is even. The graph is symmetric about the origin if the function is odd. If you need a review of even and odd functions, feel free to go to Tutorial 32: Graphs of Functions Part II.

Step 4: Find and plot any intercepts that exist.

The x-intercept is where the graph crosses the x-axis.  You can find this by setting y = 0 and solving for x. The y-intercept is where the graph crosses the y-axis.  You can find this by setting x = 0 and solving for y. If you need a review on intercepts, feel free to go to Tutorial 26: Equations of Lines.

Step 5: Find and plot several other points on the graph.

You should have AT LEAST two points in each section of the graph that is marked off by the vertical asymptotes.

Step 6: Draw curves through the points, approaching the asymptotes.

Note that your graph can cross over a horizontal or oblique asymptote, but it can NEVER cross over a vertical asymptote.